The Human Exploration of Mars
by Jim Haldenwang
written Oct. 30, 2005
revised May 5, 2019
Is it possible for human beings to visit and explore Mars? And if it is possible, is it worth doing? The human exploration of Mars is a great dream, but also a monumentally difficult undertaking. Still, the Apollo program succeeded in landing men on the moon back in the late 1960s. Traveling to Mars is a much more difficult and expensive task than a trip to the Moon, but there are ways of reducing the risks and the costs so that the journey can be made safely and affordably. With the right technologies and good planning, the dream of exploring Mars can become reality within the next two decades. This paper considers the best ideas for voyaging to Mars safely, without breaking the bank. But first, we must ask: why should we pursue such a difficult goal?
Why should humans explore Mars?
Today Mars is a cold, dry world. But we know now that the Red Planet was once warmer and wetter. Billions of years ago, there were even shallow seas on Mars. Could life have evolved there? Quite possibly. We may never know until we have thoroughly explored the Red Planet. Although the Martian surface cannot support liquid water today, it appears that there are still places on Mars where water exists underground. Also, methane gas has been observed in the Martian atmosphere. It is likely that this gas originated underneath the surface of the Red Planet. This methane could have a geologic origin, or it could have been produced by microorganisms living underground. Only by exploring Mars will we ever know if there is now or ever has been life on the Red Planet. The discovery of life on Mars, past or present, would be one of the greatest scientific discoveries of all time. Even determining that there is no life on the Red Planet would be an important discovery, for it would tell us more about how common or rare life is in the universe.
Granted there are valid scientific reasons for exploring Mars, we might then ask if we really need to send humans there. Why not rely on robots, which are much cheaper and safer? The answer is that robots have limits. Consider, for example, the task of searching for Martian fossils that may be four billion years old. The oldest fossils on Earth have been found by paleontologists in remote corners of the globe, after years of painstaking effort. Had this task been left up to robots, it is unlikely these fossils would have been discovered. Even the best of robots do not come close to matching the sophistication of human beings. This sophistication has been essential to making the most profound discoveries here on Earth.
There are other reasons to explore Mars. According to former President George W. Bush, "The desire to explore and understand is part of our character." [1] The European Space Agency is also planning to send humans to Mars. According to their first planning document, "The desire to explore is a fundamental heritage of the European people." [1] However, ESA's director of human spaceflight, Daniel Sacotte, said: "The search for territory is basic for animals and for mankind. …let's go for having the territory." [1] So, eventual colonization is another reason to visit and explore Mars. Indeed, the very long-term survival of the human species may depend upon having self-sustaining colonies on multiple worlds, as insurance against a planetary catastrophe such as a large asteroid impact or supervolcano eruption. According to the renowned astrophysicist Stephen Hawking, "It is important for the human race to spread out into space for the survival of the species. Life on Earth is at the ever-increasing risk of being wiped out by a disaster, such as sudden global warming, nuclear war, a genetically engineered virus or other dangers we have not yet thought of." [10]
Obstacles to the human exploration of Mars
Sending humans to Mars will not be easy.
There is a minimum energy requirement for a trip to Mars, determined by
the gravitational fields of the Earth, Sun, and Mars. Let's estimate
this minimum energy requirement. To do this, we must determine
the total change in velocity a rocket needs to travel from Earth to Mars.
To escape the Earth's gravity, a spaceship must attain a velocity of at least
11.2 km/s (kilometers per second) or 7 miles per second.
(This speed, 11.2 km/s, is called the Earth's escape velocity. A
spacecraft that attains this speed can coast away from the Earth forever
through the airless void of space, never falling back to Earth.) Once
free of Earth's gravity, the spacecraft needs additional velocity to reach
Mars, which is farther away from the Sun and therefore "higher up" in
the Sun's gravitational field. In order to minimize this additional
velocity, the vehicle can enter an elliptical orbit known as a Hohmann
transfer orbit. (See the accompanying image.)
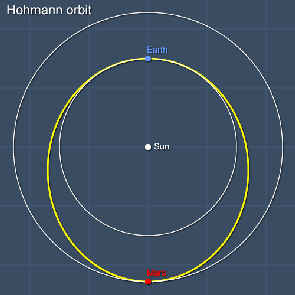Also, the journey can be timed to arrive at Mars when it is closest to
the Sun. This distance is called perihelion. At perihelion,
Mars is just 1.38 times the Earth's distance from the Sun.
Astronomers call this distance 1.38 AU, or astronomical units.
1 AU is the average distance from the Earth to the Sun, about 150 million
kilometers or 93 million miles. The additional velocity needed to reach
Mars when it is at perihelion is 2.3 km/s. It turns out that if the
spacecraft leaves Earth's vicinity at 11.4 km/s, just 0.2 km/s faster than
Earth's escape velocity, it will retain the necessary velocity of 2.3 km/s
after it has coasted far away from Earth.
As it nears Mars, the spaceship must slow down in order to enter an orbit around Mars. Once in orbit, a landing craft will have to slow down still more before it can land. It should be possible to accomplish most of this velocity reduction through aerobraking maneuvers rather than with rocket engines. In order to aerobrake, the vehicle must skim through the upper atmosphere of Mars, using frictional drag to slow it down. NASA has used this maneuver successfully in the past. [11] So, let's consider the total velocity change that must be supplied by rocket engines to travel from Earth to Mars to be 11.5 km/s. However, humans may very well prefer a plan that includes a return trip back to Earth! The escape velocity from Mars is 5.0 km/s. Plus, the spaceship will need an additional 2.6 km/s in order to enter a Hohmann transfer orbit back to Earth (assuming Mars is at its average distance from the Sun, 1.52 AU). It turns out that if the spacecraft leaves the vicinity of Mars at 5.6 km/s, just 0.6 km/s faster than the escape velocity, it will retain the necessary velocity of 2.6 km/s after it has coasted far away from Mars. Finally, once the spaceship reaches Earth, it will need to slow down so that the astronauts can land safely. Again, let's assume this can be accomplished through aerobraking, so that no additional rocket fuel will be needed.
From the above analysis, the total velocity change for a round trip to Mars that must be supplied by rocket engines is 11.5 + 5.6 = 17.1 km/s. By way of comparison, a round trip to the Moon requires a total velocity change of 11.1 + (2 × 2.4) = 15.9 km/s. (The lunar escape velocity is 2.4 km/s. Since the Moon has no atmosphere, aerobraking is not an option. A lunar landing craft must use rocket engines for both the landing and the take-off, doubling the velocity change needed.) We see that a trip to Mars and back requires just 17.1 − 15.9 = 1.2 km/s additional rocket-supplied velocity, as compared to a round trip to the Moon.
An additional velocity change of 1.2 km/s over what was accomplished by the Apollo missions back in 1969 doesn't sound too bad. However, a trip to the Moon takes 3 days, whereas a trip to Mars takes about 8 months. Also, humans on Mars will have to wait about 15 months before they can return to Earth, because the two planets must be in the correct alignment before the return journey can begin. This is because the Hohmann transfer orbit intersects the Earth's orbit at only one point, and the Earth and the returning spaceship must both be at that point at exactly the same time. The total mission time for a Martian expedition is about 2 years 8 months, whereas the Apollo 17 mission lasted just 12 days. This means the Mars journey will require about 80 times more supplies – food, air and water – than a trip to the Moon. Also, we cannot expect humans to live 16 or 17 months in a capsule the size of Apollo. The astronauts will need much larger living quarters, including exercise facilities to maintain their health in the weightless environment of space. We may also expect a larger crew to be sent to Mars, with sufficient equipment to make their 15 month stay on the Red Planet productive. Finally, extra protection from the hazardous radiation of deep space must be provided to the astronauts for their long voyage.
Let's suppose that the Mars mission will be 15 times larger than an Apollo mission to the Moon (which required one Saturn V booster rocket). Also, the additional 1.2 km/s velocity needed compared to an Apollo mission increases the amount of fuel required by 30%. (It is an unfortunate fact of rocketry that a small percentage increase in velocity requires a much larger percentage increase in fuel. This is the great problem of space travel in a nutshell.) Thus, the equivalent of about 20 Saturn V rockets will be needed to send a human expedition to Mars. These rockets will be used to lift the Mars exploration vehicle up into Earth orbit, along with all of the supplies and fuel needed for the long trip.
Solutions – technology to support the human exploration of Mars
While it is conceivable that a manned mission to Mars could be mounted using the equivalent of 20 Saturn V rockets, it is doubtful that any country or consortium of countries would care to foot the bill for such a massive undertaking. Ways must be found to reduce the cost of such a trip. How can the cost be reduced?
Aerospace engineer Robert Zubrin has proposed that a manned trip to Mars make use of the resources of the Martian atmosphere to reduce the fuel and supplies that must be sent to the Red Planet. He proposes that the expedition bring hydrogen and a small nuclear reactor to Mars. The atmosphere of Mars is 95% carbon dioxide. A chemical process known as the Sabatier reaction can be used to produce methane and water from hydrogen and Martian carbon dioxide. [2] Also, the atmospheric carbon dioxide can be decomposed to produce oxygen. Thus, methane fuel, oxygen and water can be produced on Mars, avoiding the need to transport these supplies all the way from Earth. Not having to haul the fuel needed for the return trip reduces the total mass of the mission by about an order of magnitude. In this way, the cost of the mission can be greatly reduced.
Zubrin envisions sending an unmanned ship to Mars first, before the manned expedition departs. [3] The cargo ship would land on Mars and get to work, producing methane, oxygen and water. The manned expedition would not leave Earth until all the necessary materials had been manufactured on Mars. Having supplies already stockpiled on the Red Planet will reduce the risk for the Martian explorers. Zubrin gives an example of the cargo vessel bringing 6 tonnes (6 metric tons) of liquid hydrogen, a 100 kW (kilowatt) nuclear reactor and other supplies to Mars. (One metric ton or tonne is about 2200 pounds.) Using a chemical processing unit, 108 tonnes of methane and oxygen could be produced. 96 tonnes would be used to fuel the Earth return vehicle. The remaining 12 tonnes would be used for long-range Martian ground cars. This plan reduces by a factor of 16 the amount of fuel and oxidizer that would have to be carted from Earth to Mars for the return journey. Instead of 20 Saturn V class boosters, with this on-site refueling plan the Martian mission could be accomplished with the equivalent of just two or three Saturn Vs.
SpaceX wants to use methane fuel in the near future. They want to explore and colonize Mars. [8] In order to accomplish this great vision, they are developing a new rocket engine, the Raptor. Raptor is designed to use methane. [9] Early indications are that methane will prove to be an excellent rocket fuel, with several advantages over existing fuels. Methane is a high-performance, non-toxic rocket fuel that is easier to handle and store than hydrogen. Because it is cleaner burning than kerosene, methane is well suited for reusable rocket engines. Another big advantage of methane fuel is that it can be readily obtained throughout the solar system, allowing interplanetary spaceships to refuel en route.
Another excellent idea to reduce the cost and increase the safety of a human expedition to Mars is to use electric propulsion. Electric rockets can replace chemical propulsion for the deep space portion of the trip, reducing the amount of fuel needed. The fuel efficiency of a rocket depends upon its exhaust velocity. To achieve the required velocity change, a rocket needs less fuel or propellant if its exhaust velocity is higher. Unfortunately, chemical rockets are limited to an exhaust velocity of about 4.5 km/s. This limitation can be overcome with electric rockets. Currently, the most practical version of the electric rocket is the ion rocket. [4]
The ion rocket makes use of ions, which are charged atoms that can be manipulated by electric fields. Typically, atoms of the inert gas xenon are used. These atoms are turned into ions by stripping them of their outer electrons, which leaves them with a positive charge. In the ion engine, electric fields are used to accelerate positively charged ions to very high speed. Ion rockets have been flown on deep space missions with an exhaust velocity of 30 km/s, more than six times higher than the best chemical rockets.
The Dawn deep space probe, launched in late 2007, was powered by ion engines. [7] Dawn journeyed to the asteroid Vesta and arrived there in 2011. After orbiting for over a year and conducting scientific studies, Dawn departed Vesta on Sept. 5, 2012. This intrepid little spacecraft then voyaged on to its next destination, the dwarf planet Ceres. Dawn entered orbit around Ceres in March, 2015. In order to accomplish this unprecedented journey to two worlds, Dawn's ion engines achieved a total velocity change of about 11.5 km/s, or 25,700 mph. This was nearly equal to the velocity provided by Dawn's huge Delta launch rocket. Dawn would have needed to carry more than a hundred tons of chemical fuel to accomplish its voyage of exploration to Vesta and Ceres. Instead, Dawn carried less than half a ton of xenon propellant for its thrifty ion engines.
Ion rockets have proven to be very reliable, and the technology is relatively simple and safe. One disadvantage of the ion drive is that it produces very low thrust, and cannot be used to lift off from the surface of a planet. Once in space, however, the ion rocket is a very efficient and safe way to travel from Earth orbit to Mars orbit and back again.
Why is the thrust of the electric rocket so low? Newton's laws of motion tell us there is an inescapable trade-off between fuel efficiency and thrust. For a given power level, fuel efficiency and thrust are inversely related. Rockets with greater fuel efficiency produce less thrust. The formula, derived in appendix 2 of this paper, is:
power = ½ thrust × exhaust velocity
Higher exhaust velocity is equivalent to greater fuel efficiency, as explained in appendix 2. Rockets normally operate at maximum power. Therefore, at a fixed (maximum) power level, higher exhaust velocity (fuel efficiency) means lower thrust. To illustrate this trade-off, let's consider an example. Suppose an ion engine has an exhaust velocity of 50 km/s (as seems likely in the near future). Further suppose that this engine (or bank of engines) is powered by a 15 MW (megawatt) nuclear reactor and effectively utilizes 80% of this power. Applying the above formula, the thrust is just 480 newtons, or 108 pounds. (See appendix 2 for the details of this calculation.) For a spaceship weighing 100 tonnes, a thrust of 480 newtons is less than 0.05% of the thrust needed to lift off from the surface of the Earth! For this reason, ion drives cannot be used to lift off from planetary surfaces. (Incidentally, this also applies to advanced rockets of the far future, such as fusion or antimatter rockets – see appendix 1 for details.)
Although the ion rocket is not suitable for planetary operations, in deep space electric propulsion is superior to chemical rockets. The ion engine can run continuously for months or years, eventually producing a tremendous increase in velocity. To see this, let's return to the example of the 100 tonne spaceship, powered by ion engines that produce a total thrust of 480 newtons. By Newton's second law (F = ma), the acceleration of a spaceship is equal to the thrust of its engines divided by the mass of the ship. So, applying a thrust of 480 newtons to a 100 tonne vehicle will produce an acceleration of only 0.0048 m/s/s (meters per second per second), or about 0.00049 g. (1 g, read "one gee," is the acceleration due to gravity on the surface of the Earth, about 9.8 m/s/s.) Applied over a period of months, however, even this very slight acceleration can produce a huge increase in the ship's velocity. For example, in 5 months an acceleration of just 0.00049 g will produce the fantastic velocity increase of 63 km/s (nearly 40 miles per second)! Coupled with nuclear power, the electric rocket can make manned interplanetary travel feasible.
The ESA is planning to use ion propulsion in their future manned Mars program. However, Europe is not willing to consider nuclear power. Instead, they plan to use solar power. Unfortunately, the power-to-weight ratio of solar panels is much less than that of light-weight nuclear reactors. This means that a solar-electric rocket with the same mass as a nuclear-electric rocket will be much less powerful, and therefore will take much longer to reach its destination. Using a 10,000 square foot array of solar cells, European physicist Jose Antonio Gonzales del Amo estimates the ion engines will produce about 10 newtons of thrust, and will take five years to deliver an 11-ton cargo payload to Mars. [5] The European plan is to use ion propulsion for an unmanned cargo ship and to send humans in a faster chemical-powered spaceship after the cargo ship has reached Mars. Gonzales estimates the use of ion propulsion will double the cargo that can be sent to Mars affordably.
Because of their continuous, low-thrust acceleration, spacecraft driven by electric rockets do not follow the elliptical transfer orbits used by chemically-propelled spacecraft (which coast most of the way). Instead, they follow spiral paths. An electric rocket spirals around a planet in ever-larger orbits until escape velocity is attained. Once free of the planet's gravity, the ion-powered vehicle follows a spiral trajectory away from the Sun. At about the halfway point of its journey, the spaceship turns around and begins decelerating. It must slow down enough so that it can enter orbit around the destination planet.
Currently, ion engines use the heavy inert gas xenon as their propellant. However, if an ion-propelled spaceship is to make the return journey from Mars back to Earth, it could be refueled with the lighter inert gas argon, which is present in the air of Mars. While there are disadvantages to using argon in place of xenon propellant, there is also the great advantage of not having to cart it all the way from Earth to Mars. Of course, the argon would have to be transported from the surface of Mars into orbit by a chemical rocket. Presumably this chemical rocket would use methane fuel, also obtained from the Martian atmosphere.
Conclusion
Do the benefits of a trip to Mars justify the cost of such a journey? First, let's consider the cost. According to Robert Zubrin, in 1989, prior to considering his Mars Direct plan, NASA estimated the cost of a manned trip to Mars at $400 billion. After adopting Zubrin's concept of utilizing the Martian atmosphere, NASA revised its estimate down to $50 billion in the late 1990s. [6] Utilizing electric propulsion could further reduce the cost by a factor of two.
The benefits of the human exploration of Mars are harder to quantify. We cannot put a dollar figure on the human desire to explore, our thirst for knowledge, or the opportunity to become a multi-planet, spacefaring civilization. However, these benefits are real and substantial. One day, humans will set foot on Mars.
Appendix 1: The problem with fusion rockets (and science fiction stories!)
I stated above that advanced rockets of the far future, such as fusion rockets, will not be able to lift off from planetary surfaces. I better defend this statement, so contrary to so many science fiction stories! It all goes back to this simple formula, derived in appendix 2: power = ½ thrust × exhaust velocity. Suppose we have a 100 tonne fusion rocket, with a fusion engine capable of producing 100 GW (gigawatts) of power. This enormous power output is equivalent to all of the commercial nuclear power plants in the U.S. – combined! Still, this is the far future, so let's suppose this is possible. The maximum possible exhaust velocity of a fusion engine is 30,000 km/s (one-tenth the speed of light). This enormous exhaust velocity means the fusion engine will be fantastically fuel efficient, capable of powering interstellar missions. However, using the above formula, we can calculate the thrust of this fusion rocket to be only 6700 newtons or 1500 pounds – less than one percent of the thrust needed for our 100 tonne rocket to be able to lift off from Earth!
So how could a giant Saturn V rocket ever get off the ground? The key is the exhaust velocity – by reducing the exhaust velocity, the thrust can be increased (at the cost of fuel efficiency). To illustrate, the first stage of the Saturn V rocket put 48 GW of power into its rocket exhaust – equal to the power produced by 48 commercial nuclear power plants! The exhaust velocity of this rocket was 2.8 km/s. Using the above formula, the thrust works out to be 34 million newtons or 7.7 million pounds – enough to overcome Earth's gravity and send Neil Armstrong to the Moon!
In order for an advanced fusion rocket of the far future to generate enough thrust to lift off from a planetary surface (or to escape from space pirates), the rocket will have to carry a large amount of propellant (hundreds of tons), which the fusion engine could heat up and vent out the rocket nozzles at a modest exhaust velocity, say 10 km/s. The propellant could be obtained from a planet's atmosphere or seas.
Appendix 2: Derivation of the formula power = ½ thrust × exhaust velocity [12]
Thrust is another word for force. By Newton's second law,
F = ma
In this case, F is the thrust of the rocket exhaust, m is the mass of the exhaust gas (or consumed fuel) and a is the acceleration of the exhaust gas. We can rewrite this formula as
T = ma = m(v/t) = (m/t)v
where T is the thrust, m/t is the rate of fuel consumption (mass consumed per unit time), and v is the exhaust velocity. In this form, we see that the thrust is equal to the rate of fuel consumption times the exhaust velocity. For a given thrust, increasing the exhaust velocity decreases the rate of fuel consumption, which means greater fuel efficiency. Now the power P of the rocket exhaust is equal to the kinetic energy of the exhaust per unit time, or
P = ½(mv²)/t = ½ [(m/t)v] v = ½ T v
or power = ½ thrust × exhaust velocity. For a fixed amount of power put into the rocket exhaust, increasing the exhaust velocity (and therefore the fuel efficiency) decreases the thrust. This simple formula is the key to understanding the future of space travel, which will be dominated by low-thrust propulsion.
For the example given earlier in this paper (Why is the thrust of the electric rocket so low?), we first solve our formula for thrust T. Then
T = 2P/v = 2 × (0.80 × 15,000,000)/50,000 = 480 newtons
Since there are 4.45 newtons per pound, this is equivalent to 108 pounds of thrust.
References
- Fred Guterl, The Race to Mars, Discover magazine, November, 2005, p. 63.
- Robert Zubrin, Entering Space: Creating a Spacefaring Civilization, Tarcher/Putnam, 1999, p. 153.
- Ibid., p. 102.
- https://en.wikipedia.org/wiki/ion_thruster.
- Fred Guterl, The Race to Mars, Discover magazine, November, 2005, p. 65.
- Robert Zubrin, Entering Space: Creating a Spacefaring Civilization, Tarcher/Putnam, 1999, p. 104.
- http://www.nasa.gov/mission_pages/dawn/main/index.html.
- https://en.wikipedia.org/wiki/BFR_(rocket).
- https://en.wikipedia.org/wiki/Raptor_(rocket_engine_family).
- http://www.msnbc.msn.com/id/13293390/.
- http://mars.jpl.nasa.gov/msp98/orbiter/aerobrake.html.
- Arthur C. Clarke, Interplanetary Flight, Berkley, 1960, p. 157.